楕円を次のように定義する。
平面上の2定点からの距離の和が一定値であるような点全体の集まりを楕円と呼ぶ。
2定点のことを楕円の 焦点と呼ぶ。2定点が一致したときは、上の定義を満たす点の集まりは円になり、そのときも楕円の特殊な場合と考えることもできるが、しばらくその場合は考えないことにする。
2定点から距離が一定の点をとっていくと例えば、左下の図のようになる。それに対して、右下のように、2つの焦点の中点に原点をとり、2つの焦点がともにx軸上にのるように座標系をとると、簡単に表すことができる。この座標系の取り方で楕円を方程式で表したときを標準形と呼ぶことにする。
焦点の座標を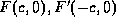
、焦点までの距離の和を2aとすると、まず、 a
>cが成り立っていることに注意する。なぜなら、焦点までの距離の和2a
は、焦点間の距離2cよりも必ず大きいからである。このとき、楕円の方程式は、
となる。ただし、bは、
を満たす正数である
証明)
となる
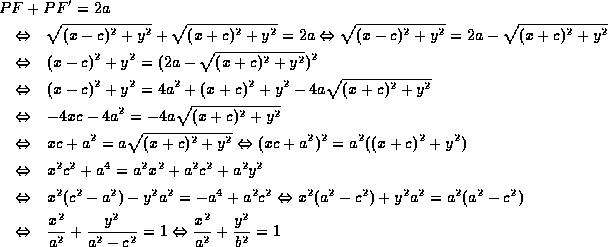
Q.E.D.
これより、楕円のx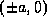切片は
、
y切片は
となることが容易にわかるであろう。このとき、a >
bとなることに注意する。2aを値を長径、2bの値を短径と呼ぶ。
もし、b>aならば、X=y,Y=xと等長変換で変換してやることによって、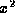 
の係数と、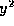
の係数を取り換えることができる。このとき、焦点を標準形に照らしあらせて考えると、XY座標上で焦点はX軸上、すなわち、
xy座標で考えると焦点は、y軸上にきて、縦長の楕円になる。まとめると、 b>aのとき、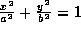
は、焦点が、 
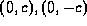となるような楕円である。ただし、cは、
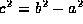となるような数である。
楕円の方程式も、放物線と同じように、二つの焦点の中心に原点が来るように表示されていないときは、そうなるように平行移動すると標準形に持っていくことができる。たとえば、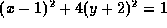
という方程式があったときは、
X=x-1,Y=y+2という変換(平行移動)を行なうと、楕円の 形を変えることな く標準形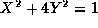
で表示できる。よって、a=1で
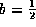なので、 a>bを満たす。よって、
となり、焦点は、XY座標で
となる。x=X+1,y=Y-2を利用して、これをxy座標で書くと、焦点は
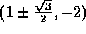となる。
楕円の式に関しては、上のように平行移動を利用して、標準形に持っていく変換のほかに、楕円を円にしてしまう変換も重要である。これは、たとえば、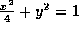 
という楕円の式があったときに、これを 
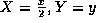と変換することにより、
という円に変換することができる。しかし、この変換は、x軸方向だけ、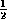
倍に縮める変換であり、等長変換ではないので、長さが保存されない。焦点と楕円の関係は長さを使って書かれるので、このような変換では焦点は焦点にうつらないことに注意する。では、どのようなときにこのような変換が役に立つかというと、この変換で保存されるような性質が問題になっているときである。たとえば、これは1次変換であるので、線分の比が保存される。たとえば、うつされる前に、中点だったものは、うつされたあとも中点になっていることなどがわかる。ほかには、逆変換を持つような1次変換では、接線は接線に写るので、接線の問題でも、楕円を円に写して解くとよい。うまく円の対称性を利用して問題をとき、得られた結果を、もとの座標系の言葉に変換しなおして、答とすればよいのである。具体的には問題を解いているうちに身につくと思われる。
最後に楕円のパラメータ表示について軽くふれる。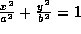 
という楕円なら、 
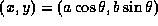とパラメータ表示できる。これは、この楕円が、
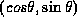とパラメータ表示される円を、
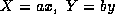で変換したものであることからもわかる。注意することは、 
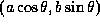の中の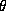
が楕円の図のなかで意味をなす量では、既になくなっているということである。すなわち、x軸正の向きと、 
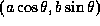の向きのなす角は一般には、
とはならない。これは、
が角度を保存しないような変換であることによる。
Kenji Kashiwabara